No post anterior vimos que a eficiência se mede no número de etapas que o algoritmo leva para ser concluído. No entanto, apenas dizer que um programa leva N etapas é um modo muito simplista de definir complexidade.

Cientistas da computação cunharam um conceito vindo da matemática para definir eficiência e complexidade de algoritmos. Esse conceito é conhecido como Notação Big O, ou, somente, Notação O.

Apesar do Big O ser um conceito matemático, não é nossa intenção aqui se aprofundar em termos e fórmulas matemáticas, e sim, usar uma forma de ver a complexidade de algoritmos de uma maneira mais inclusiva. Mas não se engane. A matemática é a base de tudo que fazemos, mas por hora, vamos deixar fórmulas complexas para os cientistas.

O(1)

Vimos que a operação de leitura leva apenas uma etapa, não importando o tamanho do array. A Notação Big O que expressa a eficiência da operação de leitura é: O(1)

Essa notação pode ser pronunciada como “Big O de 1” ou, como prefiro, “O de 1”. O(1) indica que, não importando o tamanho da estrutura de dados, a operação sempre irá levar uma única etapa.

Mesmo que um computador antigo leve 5 minutos para executar a operação, e um hardware atual leve 1 microssegundo, o algoritmo levará apenas uma etapa para ser finalizado. Lembre-se que não medimos eficiência com velocidade e sim com número de etapas. As operações de inserção e deleção também são O(1).

O(N)

Vimos que a pesquisa linear pode levar N etapas para ser concluída. Para procurar por um determinado elemento, o algoritmo irá checar cada célula do array até encontrá-lo. No pior cenário, um array de N elementos irá precisar de N etapas para ser percorrido.

Para expressar a complexidade da pesquisa linear usamos a expressão: O(N)

Podemos dizer que a pesquisa linear é “O de N”. Esse é o jeito mais bonito de dizer que para um array de N elementos, o algoritmo poderá levar N etapas.

Existe um ponto importante sobre a notação O(1). Mesmo que um algoritmo leve 5 etapas, ele pode ser considerado O(1). O que importa é que ele continue com 5 etapas independente do tamanho do array. Se para um array de 100 elementos o algoritmo levar 5 etapas, e para um array de 10.000 elementos também levar 5 etapas, então podemos dizer que o algoritmo é O(1). Isso porque a eficiência se mantém constante com o tempo. O(1) indica que o número de etapas de um algoritmo não muda à medida que a quantidade de dados cresce.

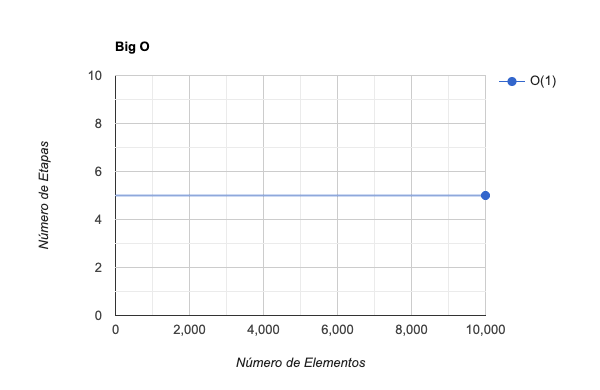
Enquanto O(1) é constante, O(N) é uma grandeza linear.

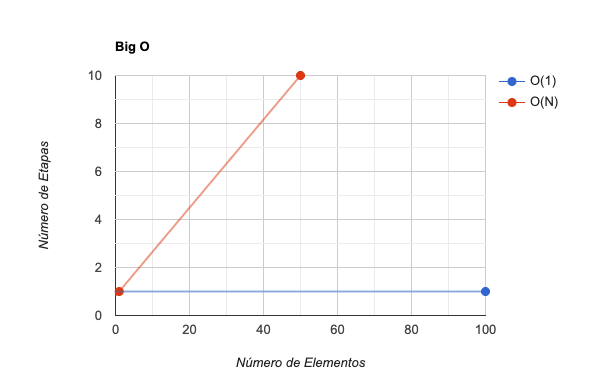
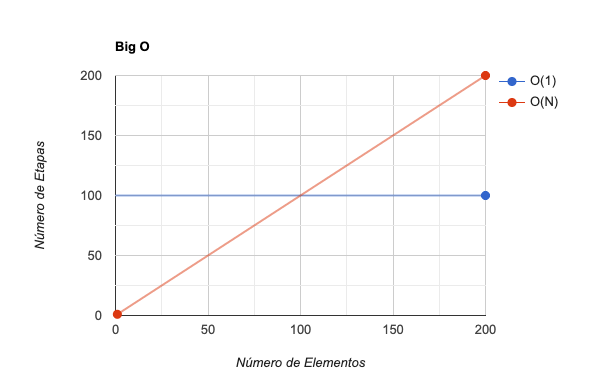
A Notação O leva em consideração o quão eficiente o algoritmo se manterá à medida que a quantidade de dados aumenta. Levando isso em conta, mesmo que um algoritmo O(1) sempre leve 100 mil etapas, ele ainda será considerado mais eficiente que O(N). Isso porque O(N) é linear, logo, em algum momento, o algoritmo O(N) será menos eficiente que O(1). O Big O não se importa em que momento isso irá acontecer. O fato é que, quando ocorrer, O(1) será mais eficiente que O(N) para sempre.

O(log N)

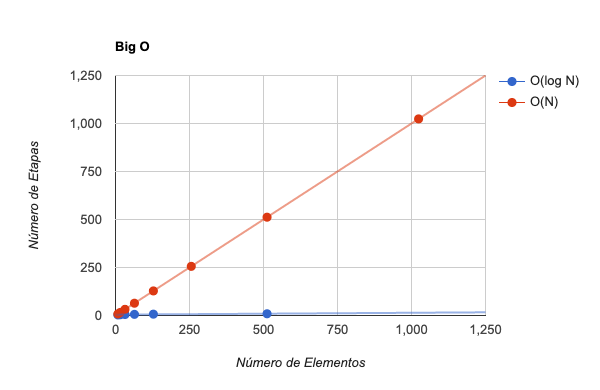
A pesquisa binária é muito mais eficiente que a pesquisa linear à medida que a quantidade de dados aumenta.

Para expressar a eficiência da pesquisa binária usamos: O(log N)

Pronunciamos “O de log de N”.

Parece que as coisas começam a se complicar. Entramos em uma escala logarítmica. Dessa vez não tem jeito. Vamos precisar entender, ou lembrar, o que é um logaritmo. Parece que finalmente nós, que não somos matemáticos, iremos usar logaritmo para algo útil em nossas vidas. Mas não se preocupe, vamos tentar fazer isso da forma mais simples possível.

Logaritmo é a operação inversa da exponenciação. $2^4$ equivale a 2x2x2x2=16. O inverso disso é expresso em:

$log{_2}{16}$

Podemos interpretar a expressão da seguinte forma: quantas vezes multiplicar 2 por ele mesmo para que o resultado seja 16? O resultado é 4 vezes, pois 2x2x2x2 é igual a 16. Logo, $log{_2}{16}$ = 4.

Outra maneira de explicar $log{_2}{16}$ é: quantas vezes dividir 16 por 2 para que o resultado seja 1.

16 / 2 / 2 / 2 / 2 = 1

O resultado é 4 vezes.

O(log N) é o mesmo que O($log{_2}{N}$). Isso significa que, para N elementos, o algoritmo levaria $log{_2}{N}$ etapas. Para 16 elementos, o algoritmo levaria 4 etapas, pois $log{_2}{16}$ = 4. Esse é o comportamento de se dividir o número de elementos pela metade até se chegar no elemento pesquisado. É exatamente o que ocorre na pesquisa binária. O(log N) é mais eficiente que O(N), pois a cada vez que dobramos o número de elementos aumentamos apenas uma etapa.

Show me the code

Agora chegamos em um momento em que é necessário analisarmos código fonte. Pois o objetivo da Notação Big O é fazer com que possamos analisar e melhorar a performance de programas do dia a dia. Para isso, iremos usar um exemplo de algoritmo de ordenação. O algoritmo apresentado é bastante grosseiro, daqueles escritos por programadores que pensam com o dedo. Algoritmos mais sofisticados exigem tempo e dedicação. Quando pensamos com o dedo, escrevemos soluções problemáticas. De fato, dificilmente usamos algoritmos de ordenação hoje em dia, pois as linguagens de programação modernas já possuem métodos de ordenação bastante eficientes em suas apis. Mas aqui, iremos usar este exemplo para fins didáticos.

  def sort(array)
    array_length = array.size
    return array if array_length <= 1

    loop do
      swapped = false

      (array_length-1).times do |i|
        if array[i] > array[i+1]
          array[i], array[i+1] = array[i+1], array[i]
          swapped = true
        end
      end

      break if not swapped
    end

    array
  end

O método sort, escrito em ruby, ordena elementos em um array usando dois passos. O primeiro é uma comparação entre um elemento e seu adjacente. O segundo passo é a troca de lugares entre elementos, caso o primeiro elemento seja maior que o próximo.

Esse, talvez seja o algoritmo de ordenação mais simples de se implementar, pois não é necessário pensar muito na solução. O bloco loop irá iterar até que o array esteja ordenado. Isso é controlado pela variável swapped. Quando swapped for false, significa que não haverá mais nenhuma troca entre elementos. Logo, o array estará ordenado. Muito simples.

Muitos conhecem esse algoritmo como Bubble Sort.

Como dito anteriormente, o algoritmo possui dois passos: comparação entre elementos e a troca de posição. Na análise de complexidade, sempre consideramos a pior das hipóteses, que para o nosso cenário é um array na ordem inversa.

Para um array de 5 elementos, teremos 10 comparações e 10 trocas, ou seja, 20 etapas.

Para um array de 10 elementos na ordem inversa, teremos 45 comparações e 45 trocas, ou seja, 90 etapas.

Para um array de 80 elementos teremos 6320 etapas.

Se analisarmos o crescimento do número de etapas, veremos uma curva exponencial. Por exemplo:

• 5 elementos, 20 etapas, $5^2$.
• 10 elementos, 90 etapas, aproximadamente $10^2$.
• 80 elementos, 6320 etapas, aproximadamente $80^2$.
• N elementos, $N^2$ etapas.

Concluímos que o Bubble Sort é O($N^2$).

Perceba que no loop externo, precisamos iterar N vezes. E a cada iteração do loop externo, precisamos iterar N vezes. Logo, o número de etapas é N x N = $N^2$.

Não é à toa que O($N^2$) indica loops aninhados. Então, sempre que você precisar fazer loops aninhados, perceba que, talvez você esteja escrevendo um algoritmo lento.

Mais a frente iremos verificar outros aspectos do Big O. Até lá.

• Parte 1: Complexidade de algoritmos - Estrutura de Dados
• Parte 2: Notação Big O para não matemáticos